MEMO 2007 pojedinačno problem 2
Kvaliteta:
Avg: 3,6Težina:
Avg: 6,0 A set of balls contains  balls which are labeled with numbers
balls which are labeled with numbers 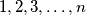 . We are given
. We are given  such sets. We want to colour the balls with two colours, black and white in such a way, that
such sets. We want to colour the balls with two colours, black and white in such a way, that
(a) the balls labeled with the same number are of the same colour,
(b) any subset of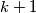 balls with (not necessarily different) labels
balls with (not necessarily different) labels 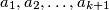 satisfying the condition
satisfying the condition 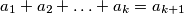 , contains at least one ball of each colour.
, contains at least one ball of each colour.
Find, depending on the greatest possible number
the greatest possible number  which admits such a colouring.
which admits such a colouring.
 balls which are labeled with numbers
balls which are labeled with numbers 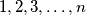 . We are given
. We are given  such sets. We want to colour the balls with two colours, black and white in such a way, that
such sets. We want to colour the balls with two colours, black and white in such a way, that (a) the balls labeled with the same number are of the same colour,
(b) any subset of
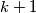 balls with (not necessarily different) labels
balls with (not necessarily different) labels 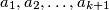 satisfying the condition
satisfying the condition 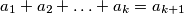 , contains at least one ball of each colour.
, contains at least one ball of each colour. Find, depending on
 the greatest possible number
the greatest possible number  which admits such a colouring.
which admits such a colouring. Izvor: Srednjoeuropska matematička olimpijada 2007, pojedinačno natjecanje, problem 2
 Školjka
Školjka 
