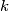
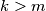
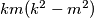
Let and , with , be positive integers such that the number is divisible by . Prove that .
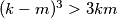
%V0
Let $k$ and $m$, with $k > m$, be positive integers such that the number $km(k^2 - m^2)$ is divisible by $k^3 - m^3$. Prove that $(k - m)^3 > 3km$.
Izvor: Srednjoeuropska matematička olimpijada 2011, pojedinačno natjecanje, problem 4
Školjka 
and 
, with 
, be positive integers such that the number 
is divisible by 
. Prove that 
.