Ako imamo cijeli broj  i prirodni broj
i prirodni broj  , te brojeve mozemo cjelobrojno podjeliti (podjeliti tako da dobijemo cijeli broj i ostatak), to jest
, te brojeve mozemo cjelobrojno podjeliti (podjeliti tako da dobijemo cijeli broj i ostatak), to jest  mozemo zapisati kao
mozemo zapisati kao 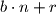 za neke cijele brojeve
za neke cijele brojeve  i
i  , take da je
, take da je 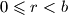 . (Tvrdnja 1)
. (Tvrdnja 1)
Taj zapis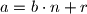 je jedinstven, odnosno postoji tocno jedan
je jedinstven, odnosno postoji tocno jedan  i tocno jedan
i tocno jedan  takvi da je
takvi da je 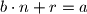 . (Tvrdnja 2)
. (Tvrdnja 2)
Tako, mozemo reci da je kongruentan
kongruentan  modulo
modulo  , a to zapisujemo
, a to zapisujemo 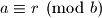
Ovaj zapis je lijep jer sa njime mozemo lagano baratati, neka od njegovih svojstava su:
 Ako je
Ako je 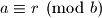 i
i 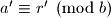 onda je
onda je 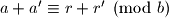 (Tvrdnja 3)
(Tvrdnja 3)
 Ako je
Ako je 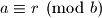 i
i 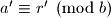 onda je
onda je 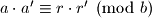 (Tvrdnja 4)
(Tvrdnja 4)
 Dijeljenje je definirano ako su broj kojim djelimo i borj ciji modul gledamo relativno prosti, no za sada cemo ga izbjegavati
Dijeljenje je definirano ako su broj kojim djelimo i borj ciji modul gledamo relativno prosti, no za sada cemo ga izbjegavati
 Ako je
Ako je 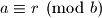 onda je
onda je 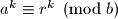 (Tvrdnja 5)
(Tvrdnja 5)
Dokaz tvrdnje 1:
Neka je najveci cijeli broj takav da je
najveci cijeli broj takav da je 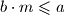 . Tada je
. Tada je 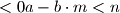 . Oznacimo sada izraz (
. Oznacimo sada izraz (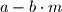 ) sa
) sa  (to jest neka je
(to jest neka je 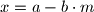 ). Primjetimo da je
). Primjetimo da je 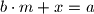 pa ako je
pa ako je 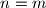 i
i 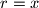 , tada je
, tada je 
Dakle takvi brojevi postoje.
Dokaz tvrdnje 2:
Pretpostavimo da postoje 2 para takvih brojeva. Dakle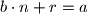 i
i 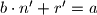 . Postoje tri moguca slucaja:
. Postoje tri moguca slucaja:
 Prvi slucaj:
Prvi slucaj:
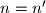 ,
, 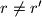
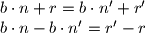
A kako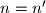
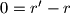
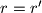 Kontradikcija
Kontradikcija
 Drugi slucaj:
Drugi slucaj:
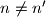 ,
, 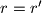
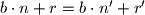
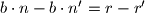 A kako
A kako 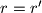
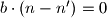
Kako je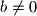 zakljucujemo
zakljucujemo 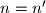 Kontradikcija
Kontradikcija
 Treci slucaj:
Treci slucaj:
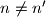 ,
, 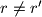
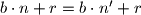
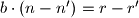
Kako je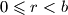 i
i 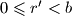 Znamo da
Znamo da 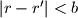 no
no 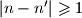 pa je
pa je 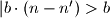
Dakle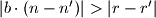 Sto je nemoguce ako su ti brojevi jednaki. Kontradikcija.
Sto je nemoguce ako su ti brojevi jednaki. Kontradikcija.
Kako smo isprobali sve slucajeve kada su ti brojevi razliciti, i u svakome dosli do kontradikcije, ocito mora vrijediti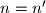 i
i 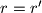
Dokaz tvrdnje 3:
Iz definicije kongruencija vidimo da je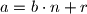 i
i 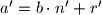 za neke
za neke  i
i 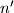 . Broj
. Broj 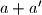 tada mozemo prikazati kao
tada mozemo prikazati kao 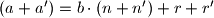 I sada, ponovnim koristenjem definicije dobivamo da je newline
I sada, ponovnim koristenjem definicije dobivamo da je newline 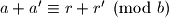
Dokaz tvrdnje 4: newline Iz definicije kongruencija vidimo da je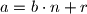 i
i 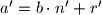 za neke
za neke  i
i 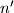 . Broj
. Broj 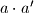 tada mozemo prikazati kao
tada mozemo prikazati kao 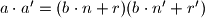 Mnozenjem i sredivanjem ovog izraza dobivamo newline
Mnozenjem i sredivanjem ovog izraza dobivamo newline 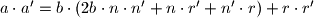 Ponovnim koristenjem definicije dobivamo
Ponovnim koristenjem definicije dobivamo 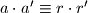
Dokaz tvrdnje 5:
Ova tvrdnja trivijalno slijedi iz tvrdnje 4 primjenjene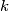 puta.
puta.
 i prirodni broj
i prirodni broj  , te brojeve mozemo cjelobrojno podjeliti (podjeliti tako da dobijemo cijeli broj i ostatak), to jest
, te brojeve mozemo cjelobrojno podjeliti (podjeliti tako da dobijemo cijeli broj i ostatak), to jest  mozemo zapisati kao
mozemo zapisati kao 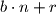 za neke cijele brojeve
za neke cijele brojeve  i
i  , take da je
, take da je 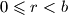 . (Tvrdnja 1)
. (Tvrdnja 1) Taj zapis
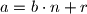 je jedinstven, odnosno postoji tocno jedan
je jedinstven, odnosno postoji tocno jedan  i tocno jedan
i tocno jedan  takvi da je
takvi da je 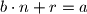 . (Tvrdnja 2)
. (Tvrdnja 2)Tako, mozemo reci da je
 kongruentan
kongruentan  modulo
modulo  , a to zapisujemo
, a to zapisujemo 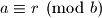
Ovaj zapis je lijep jer sa njime mozemo lagano baratati, neka od njegovih svojstava su:
 Ako je
Ako je 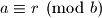 i
i 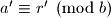 onda je
onda je 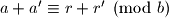 (Tvrdnja 3)
(Tvrdnja 3) Ako je
Ako je 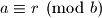 i
i 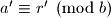 onda je
onda je 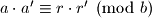 (Tvrdnja 4)
(Tvrdnja 4) Dijeljenje je definirano ako su broj kojim djelimo i borj ciji modul gledamo relativno prosti, no za sada cemo ga izbjegavati
Dijeljenje je definirano ako su broj kojim djelimo i borj ciji modul gledamo relativno prosti, no za sada cemo ga izbjegavati Ako je
Ako je 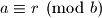 onda je
onda je 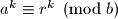 (Tvrdnja 5)
(Tvrdnja 5)Dokaz tvrdnje 1:
Neka je
 najveci cijeli broj takav da je
najveci cijeli broj takav da je 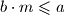 . Tada je
. Tada je 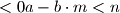 . Oznacimo sada izraz (
. Oznacimo sada izraz (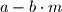 ) sa
) sa  (to jest neka je
(to jest neka je 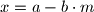 ). Primjetimo da je
). Primjetimo da je 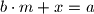 pa ako je
pa ako je 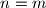 i
i 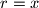 , tada je
, tada je 
Dakle takvi brojevi postoje.
Dokaz tvrdnje 2:
Pretpostavimo da postoje 2 para takvih brojeva. Dakle
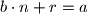 i
i 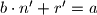 . Postoje tri moguca slucaja:
. Postoje tri moguca slucaja: Prvi slucaj:
Prvi slucaj: 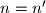 ,
, 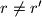
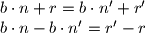
A kako
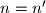
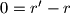
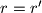 Kontradikcija
Kontradikcija Drugi slucaj:
Drugi slucaj: 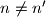 ,
, 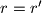
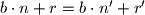
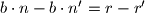 A kako
A kako 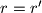
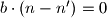
Kako je
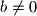 zakljucujemo
zakljucujemo 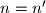 Kontradikcija
Kontradikcija Treci slucaj:
Treci slucaj: 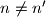 ,
, 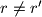
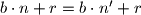
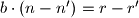
Kako je
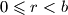 i
i 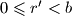 Znamo da
Znamo da 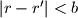 no
no 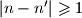 pa je
pa je 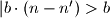
Dakle
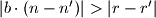 Sto je nemoguce ako su ti brojevi jednaki. Kontradikcija.
Sto je nemoguce ako su ti brojevi jednaki. Kontradikcija.Kako smo isprobali sve slucajeve kada su ti brojevi razliciti, i u svakome dosli do kontradikcije, ocito mora vrijediti
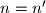 i
i 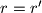
Dokaz tvrdnje 3:
Iz definicije kongruencija vidimo da je
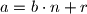 i
i 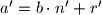 za neke
za neke  i
i 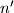 . Broj
. Broj 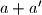 tada mozemo prikazati kao
tada mozemo prikazati kao 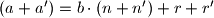 I sada, ponovnim koristenjem definicije dobivamo da je newline
I sada, ponovnim koristenjem definicije dobivamo da je newline 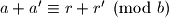
Dokaz tvrdnje 4: newline Iz definicije kongruencija vidimo da je
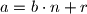 i
i 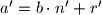 za neke
za neke  i
i 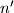 . Broj
. Broj 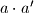 tada mozemo prikazati kao
tada mozemo prikazati kao 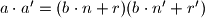 Mnozenjem i sredivanjem ovog izraza dobivamo newline
Mnozenjem i sredivanjem ovog izraza dobivamo newline 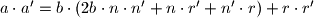 Ponovnim koristenjem definicije dobivamo
Ponovnim koristenjem definicije dobivamo 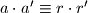
Dokaz tvrdnje 5:
Ova tvrdnja trivijalno slijedi iz tvrdnje 4 primjenjene
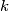 puta.
puta.  Školjka
Školjka