MEMO 2014 ekipno problem 3
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let 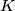 and
and 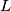 be positive integers. On a board consisting of
be positive integers. On a board consisting of 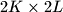 unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.
unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.
In some cases the collection of all unvisited squares forms a single rectangle. In such cases, we call this rectangle MEMOrable.
Determine the number of different MEMOrable rectangles.
Remark. Rectangles are different unless they consist of exactly the same squares.
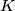 and
and 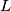 be positive integers. On a board consisting of
be positive integers. On a board consisting of 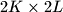 unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.
unit squares an ant starts in the lower left corner square and walks to the upper right corner square. In each step it goes horizontally or vertically to a neighbourning square. It never visits a square twice. At the end some squares may remain unvisited.In some cases the collection of all unvisited squares forms a single rectangle. In such cases, we call this rectangle MEMOrable.
Determine the number of different MEMOrable rectangles.
Remark. Rectangles are different unless they consist of exactly the same squares.
Izvor: Srednjoeuropska matematička olimpijada 2014, ekipno natjecanje, problem 3
 Školjka
Školjka 
