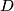
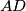
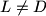
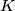
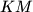
Let the incircle of the triangle touch its side at . Let the line intersect at and denote the excentre of opposite to by . Let and be the midpoints of and respectively.
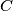
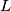
Prove that the points , , , and are concyclic.
%V0
Let the incircle $k$ of the triangle $ABC$ touch its side $BC$ at $D$. Let the line $AD$ intersect $k$ at $L \neq D$ and denote the excentre of $ABC$ opposite to $A$ by $K$. Let $M$ and $N$ be the midpoints of $BC$ and $KM$ respectively.
Prove that the points $B$, $C$, $N$, and $L$ are concyclic.
Izvor: Srednjoeuropska matematička olimpijada 2014, ekipno natjecanje, problem 6
Školjka 
of the triangle 
touch its side 
at 
. Let the line 
intersect 
and denote the excentre of 
by 
. Let 
and 
be the midpoints of 
respectively.
, 
, 
are concyclic.