Given are 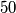 points in the plane, no three of them belonging to a same line. Each of these points is colored using one of four given colors. Prove that there is a color and at least
points in the plane, no three of them belonging to a same line. Each of these points is colored using one of four given colors. Prove that there is a color and at least 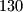 scalene triangles with vertices of that color.
scalene triangles with vertices of that color.
Given are $50$ points in the plane, no three of them belonging to a same line. Each of these points is colored using one of four given colors. Prove that there is a color and at least $130$ scalene triangles with vertices of that color.