Točno
14. travnja 2012. 12:44 (13 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
imamo a, d=a+1, P=a+2, S=a+3;
kako bi P i S po vieteovim formulama bili cijeli brojevim vrijedi
b=am
c=an
sad uvrstimo
a, a^2(m^2-4n), n, -m
a=a, n=a+2, -m=a+3 uvrstimo u a^2(m^2-4n)
dobimo:
(a^3+a^2-1)(a+1)=0
1. a=-1
2. a^3+a^2-1=0; a^3+a^2=-1; a^2(a+1)=1; tj.:
a+1=+-1 a=0; a=-2 ako uvrstimo u a^2(a+1)=1 vidjet cemo da ova jednadžba nema cjelobrojnih rješenja.
znači, a=-1
n=1
-m=2; m=-2
d=a^2(4-4)=0
-1,0,1,2; i to su jedina rješenja
kako bi P i S po vieteovim formulama bili cijeli brojevim vrijedi
b=am
c=an
sad uvrstimo
a, a^2(m^2-4n), n, -m
a=a, n=a+2, -m=a+3 uvrstimo u a^2(m^2-4n)
dobimo:
(a^3+a^2-1)(a+1)=0
1. a=-1
2. a^3+a^2-1=0; a^3+a^2=-1; a^2(a+1)=1; tj.:
a+1=+-1 a=0; a=-2 ako uvrstimo u a^2(a+1)=1 vidjet cemo da ova jednadžba nema cjelobrojnih rješenja.
znači, a=-1
n=1
-m=2; m=-2
d=a^2(4-4)=0
-1,0,1,2; i to su jedina rješenja
Ocjene: (2)
Komentari:
grga, 14. travnja 2012. 17:55
Filip_Wee, 14. travnja 2012. 16:48
grga, 14. travnja 2012. 14:34
grga, 14. travnja 2012. 14:33
treba ti bit 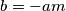 cini mi se.
cini mi se.
i.. kuzis da uvodis oznake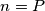 , i
, i 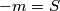
mozda bi bilo dobro da si na drzavnom napisat da se radi od jednadbi
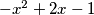
pa onda jos provjerit kao dal je to zadovoljeno, za svaki slucaj
osim toga je tocno! :)
ponovo ti saljem tvoje rjesenje u latexu.
imamo ,
, 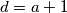 ,
, 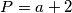 ,
, 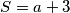 ;
;
kako bi P i S po vieteovim formulama bili cijeli brojevim vrijedi
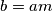
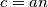
sad uvrstimo
 ,
, 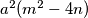 ,
,  ,
, 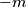
 ,
, 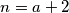 ,
, 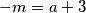 uvrstimo u
uvrstimo u 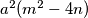
dobimo:
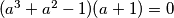
1.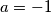
2.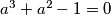 ;
; 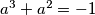 ;
;  ; tj.:
; tj.:
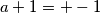
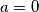 ;
; 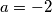 ako uvrstimo u
ako uvrstimo u  vidjet cemo da ova jednadžba nema cjelobrojnih rješenja.
vidjet cemo da ova jednadžba nema cjelobrojnih rješenja.
znači,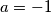
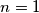
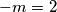 ;
; 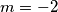
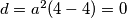
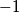 ,
, 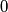 ,
, 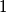 ,
, 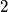 ; i to su jedina rješenja
; i to su jedina rješenja
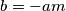 cini mi se.
cini mi se.i.. kuzis da uvodis oznake
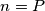 , i
, i 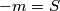
mozda bi bilo dobro da si na drzavnom napisat da se radi od jednadbi
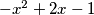
pa onda jos provjerit kao dal je to zadovoljeno, za svaki slucaj
osim toga je tocno! :)
ponovo ti saljem tvoje rjesenje u latexu.
imamo
 ,
, 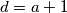 ,
, 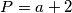 ,
, 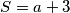 ;
;kako bi P i S po vieteovim formulama bili cijeli brojevim vrijedi
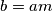
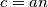
sad uvrstimo
 ,
, 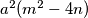 ,
,  ,
, 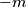
 ,
, 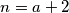 ,
, 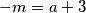 uvrstimo u
uvrstimo u 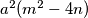
dobimo:
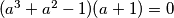
1.
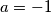
2.
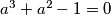 ;
; 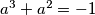 ;
;  ; tj.:
; tj.: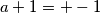
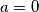 ;
; 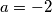 ako uvrstimo u
ako uvrstimo u  vidjet cemo da ova jednadžba nema cjelobrojnih rješenja.
vidjet cemo da ova jednadžba nema cjelobrojnih rješenja.znači,
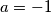
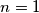
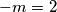 ;
; 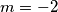
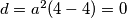
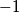 ,
, 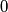 ,
, 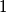 ,
, 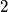 ; i to su jedina rješenja
; i to su jedina rješenja  Školjka
Školjka 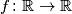 kvadratna funkcija
kvadratna funkcija 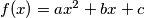 . Označimo sa
. Označimo sa 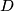 diskriminantu, sa
diskriminantu, sa  umnožak, a sa
umnožak, a sa 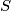 zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija
zbroj njezinih nultočaka. Pokažite da postoji samo jedna funkcija 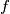 za koju su
za koju su