Neocijenjeno
23. veljače 2016. 13:32 (9 godine, 11 mjeseci)
Sakrij rješenje
Sakrij rješenje
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Podijelimo tablicu na 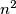 kvadrata dimenzija
kvadrata dimenzija 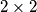 i uočimo da svaki od ovih kvadrata može sadržavati najviše 2 elementa skupa
i uočimo da svaki od ovih kvadrata može sadržavati najviše 2 elementa skupa 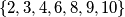 : naime, svaki je od brojeva u tom skupu djeljiv s 2 ili 3, pa među svaka tri broja iz tog skupa možemo uvijek naći dva koja imaju zajednički djelitelj. Zato se tri broja iz tog skupa ne mogu naći u
: naime, svaki je od brojeva u tom skupu djeljiv s 2 ili 3, pa među svaka tri broja iz tog skupa možemo uvijek naći dva koja imaju zajednički djelitelj. Zato se tri broja iz tog skupa ne mogu naći u 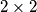 kvadrata u kojemu sva četiri polja imaju jedan zajednički vrh.
kvadrata u kojemu sva četiri polja imaju jedan zajednički vrh.
Dakle, svaki od tih kvadrata sadrži barem dva elementa skupa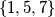 . Budući da takvih kvadrata ima
. Budući da takvih kvadrata ima 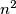 , u čitavoj se tablici članovi skupa
, u čitavoj se tablici članovi skupa 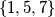 pojavljuju barem
pojavljuju barem 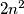 puta. Sada prema Dirichletovom principu zaključujemo kako će se jedan broj iz tog skupa u tablici pojaviti barem
puta. Sada prema Dirichletovom principu zaključujemo kako će se jedan broj iz tog skupa u tablici pojaviti barem 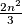 puta.
puta.
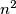 kvadrata dimenzija
kvadrata dimenzija 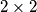 i uočimo da svaki od ovih kvadrata može sadržavati najviše 2 elementa skupa
i uočimo da svaki od ovih kvadrata može sadržavati najviše 2 elementa skupa 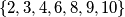 : naime, svaki je od brojeva u tom skupu djeljiv s 2 ili 3, pa među svaka tri broja iz tog skupa možemo uvijek naći dva koja imaju zajednički djelitelj. Zato se tri broja iz tog skupa ne mogu naći u
: naime, svaki je od brojeva u tom skupu djeljiv s 2 ili 3, pa među svaka tri broja iz tog skupa možemo uvijek naći dva koja imaju zajednički djelitelj. Zato se tri broja iz tog skupa ne mogu naći u 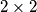 kvadrata u kojemu sva četiri polja imaju jedan zajednički vrh.
kvadrata u kojemu sva četiri polja imaju jedan zajednički vrh.Dakle, svaki od tih kvadrata sadrži barem dva elementa skupa
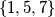 . Budući da takvih kvadrata ima
. Budući da takvih kvadrata ima 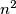 , u čitavoj se tablici članovi skupa
, u čitavoj se tablici članovi skupa 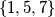 pojavljuju barem
pojavljuju barem 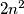 puta. Sada prema Dirichletovom principu zaključujemo kako će se jedan broj iz tog skupa u tablici pojaviti barem
puta. Sada prema Dirichletovom principu zaključujemo kako će se jedan broj iz tog skupa u tablici pojaviti barem 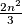 puta.
puta.  Školjka
Školjka  upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem
upisani su prirodni brojevi od 1 do 10, pri čemu su brojevi u poljima sa zajedničkim vrhom relativno prosti. Dokažite da postoji broj koji se u tablici pojavljuje barem  puta.
puta.