Točno
23. ožujka 2016. 12:54 (9 godine, 10 mjeseci)
Korisnik: matsimic
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 2. (Sakrij tekst zadatka)
Zadatak: Simulacija državnog 2016. za prvi razred zadatak 2. (Sakrij tekst zadatka)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Označimo s 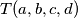 tvrdnju
tvrdnju 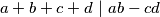 .
.
Dokazati ćemo da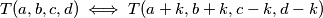 ,
, 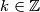

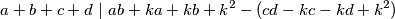
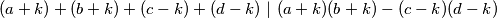
Prema tome, tvrdnja je dokazana.
Uzmimo neki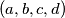 za koji vrijedi
za koji vrijedi 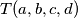 i pretpostavimo WLOG da je
i pretpostavimo WLOG da je 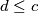 .
.
Tada vrijedi i tvrdnja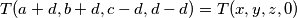 tj. vrijedi da
tj. vrijedi da 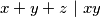 .
.
Za svaki prost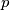 ,
, 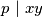 vrijedi
vrijedi 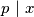 i/ili
i/ili 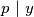 pa tako i
pa tako i 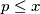 i/ili
i/ili 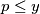 pa zbog toga i
pa zbog toga i 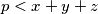 iz čega konačno zaključujemo da
iz čega konačno zaključujemo da 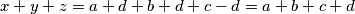 ne može biti prost broj. Zbog toga što je suma
ne može biti prost broj. Zbog toga što je suma 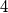 prirodna broja veća ili jednaka
prirodna broja veća ili jednaka 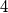 , ne može biti jednaka ni
, ne može biti jednaka ni 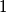 pa mora bit složen broj.
pa mora bit složen broj.
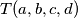 tvrdnju
tvrdnju 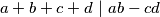 .
.Dokazati ćemo da
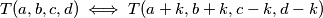 ,
, 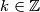

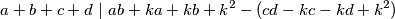
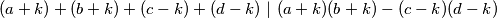
Prema tome, tvrdnja je dokazana.
Uzmimo neki
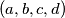 za koji vrijedi
za koji vrijedi 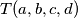 i pretpostavimo WLOG da je
i pretpostavimo WLOG da je 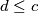 .
.Tada vrijedi i tvrdnja
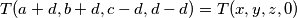 tj. vrijedi da
tj. vrijedi da 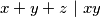 .
. Za svaki prost
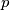 ,
, 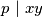 vrijedi
vrijedi 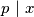 i/ili
i/ili 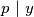 pa tako i
pa tako i 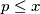 i/ili
i/ili 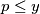 pa zbog toga i
pa zbog toga i 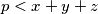 iz čega konačno zaključujemo da
iz čega konačno zaključujemo da 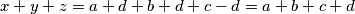 ne može biti prost broj. Zbog toga što je suma
ne može biti prost broj. Zbog toga što je suma 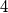 prirodna broja veća ili jednaka
prirodna broja veća ili jednaka 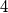 , ne može biti jednaka ni
, ne može biti jednaka ni 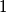 pa mora bit složen broj.
pa mora bit složen broj.  Školjka
Školjka  ,
,  ,
,  ,
, 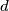 prirodni brojevi takvi da je
prirodni brojevi takvi da je 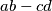 djeljiv s
djeljiv s 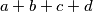 . Dokažite da je broj
. Dokažite da je broj 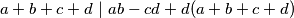 i doći do zaključka na isti način kao i ovdje uz puno manje posla.
i doći do zaključka na isti način kao i ovdje uz puno manje posla.