The function
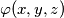
defined for all triples
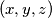
of real numbers, is such that there are two functions
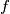
and
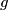
defined for all pairs of real numbers, such that
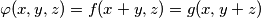
for all real numbers
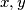
and
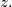
Show that there is a function
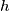
of one real variable, such that
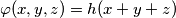
for all real numbers
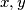
and
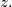
%V0
The function $\varphi(x,y,z)$ defined for all triples $(x,y,z)$ of real numbers, is such that there are two functions $f$ and $g$ defined for all pairs of real numbers, such that
$$\varphi(x,y,z) = f(x+y,z) = g(x,y+z)$$
for all real numbers $x,y$ and $z.$ Show that there is a function $h$ of one real variable, such that
$$\varphi(x,y,z) = h(x+y+z)$$
for all real numbers $x,y$ and $z.$