IMO Shortlist 1987 problem 1
Dodao/la:
arhiva2. travnja 2012. Let f be a function that satisfies the following conditions:
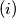
If
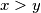
and
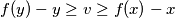
, then
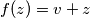
, for some number

between

and
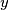
.
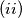
The equation
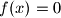
has at least one solution, and among the solutions of this equation, there is one that is not smaller than all the other solutions;
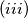
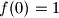
.
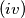
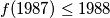
.
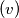
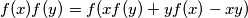
.
Find
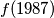
.
Proposed by Australia.
%V0
Let f be a function that satisfies the following conditions:
$(i)$ If $x > y$ and $f(y) - y \geq v \geq f(x) - x$, then $f(z) = v + z$, for some number $z$ between $x$ and $y$.
$(ii)$ The equation $f(x) = 0$ has at least one solution, and among the solutions of this equation, there is one that is not smaller than all the other solutions;
$(iii)$ $f(0) = 1$.
$(iv)$ $f(1987) \leq 1988$.
$(v)$ $f(x)f(y) = f(xf(y) + yf(x) - xy)$.
Find $f(1987)$.
Proposed by Australia.
Izvor: Međunarodna matematička olimpijada, shortlist 1987