Let
be an odd integer greater than 1 and let
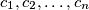
be integers. For each permutation
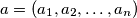
of
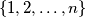
, define
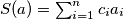
. Prove that there exist permutations
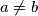
of
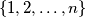
such that
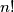
is a divisor of
.
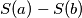
%V0
Let $n$ be an odd integer greater than 1 and let $c_1, c_2, \ldots, c_n$ be integers. For each permutation $a = (a_1, a_2, \ldots, a_n)$ of $\{1,2,\ldots,n\}$, define $S(a) = \sum_{i=1}^n c_i a_i$. Prove that there exist permutations $a \neq b$ of $\{1,2,\ldots,n\}$ such that $n!$ is a divisor of $S(a)-S(b)$.
Školjka