Consider the system
,
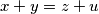
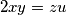
. Find the greatest value of the real constant
such that
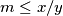
for any positive integer solution
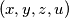
of the system, with
.
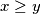
%V0
Consider the system $x + y = z + u$, $2xy = zu$. Find the greatest value of the real constant $m$ such that $m \leq x/y$ for any positive integer solution $(x,y,z,u)$ of the system, with $x \geq y$.
Školjka