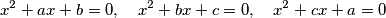
Let , , be real numbers such that for every two of the equations there is exactly one real number satisfying both of them. Determine all possible values of .
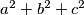
%V0
Let $a$, $b$, $c$ be real numbers such that for every two of the equations $$x^2+ax+b=0, \quad x^2+bx+c=0, \quad x^2+cx+a=0$$ there is exactly one real number satisfying both of them. Determine all possible values of $a^2+b^2+c^2$.
Izvor: Srednjoeuropska matematička olimpijada 2009, ekipno natjecanje, problem 2
Školjka 
, 
, 
be real numbers such that for every two of the equations 
there is exactly one real number satisfying both of them. Determine all possible values of 
.