MEMO 2011 pojedinačno problem 2
Kvaliteta:
Avg: 3,0Težina:
Avg: 6,0 Let 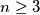 be an integer. John and Mary play the following game: First John labels the sides of a regular
be an integer. John and Mary play the following game: First John labels the sides of a regular  -gon with the numbers
-gon with the numbers 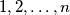 in whatever order he wants, using each number exactly once. Then Mary divides this
in whatever order he wants, using each number exactly once. Then Mary divides this  -gon into triangles by drawing
-gon into triangles by drawing 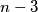 diagonals which do not intersect each other inside the
diagonals which do not intersect each other inside the  -gon. All these diagonals are labeled with number
-gon. All these diagonals are labeled with number 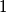 . Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those
. Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those 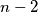 products.
products.
Determine the value of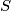 if Mary wants the number
if Mary wants the number 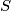 to be as small as possible and John wants
to be as small as possible and John wants 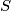 to be as large as possible and if they both make the best possible choices.
to be as large as possible and if they both make the best possible choices.
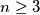 be an integer. John and Mary play the following game: First John labels the sides of a regular
be an integer. John and Mary play the following game: First John labels the sides of a regular  -gon with the numbers
-gon with the numbers 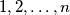 in whatever order he wants, using each number exactly once. Then Mary divides this
in whatever order he wants, using each number exactly once. Then Mary divides this  -gon into triangles by drawing
-gon into triangles by drawing 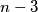 diagonals which do not intersect each other inside the
diagonals which do not intersect each other inside the  -gon. All these diagonals are labeled with number
-gon. All these diagonals are labeled with number 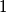 . Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those
. Into each of the triangles the product of the numbers on its sides is written. Let S be the sum of those 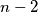 products.
products.Determine the value of
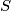 if Mary wants the number
if Mary wants the number 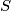 to be as small as possible and John wants
to be as small as possible and John wants 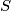 to be as large as possible and if they both make the best possible choices.
to be as large as possible and if they both make the best possible choices. Izvor: Srednjoeuropska matematička olimpijada 2011, pojedinačno natjecanje, problem 2
 Školjka
Školjka