Let
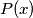
and
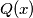
be two polynomials with integer coefficients, such that no nonconstant polynomial with rational coefficients divides both
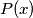
and
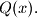
Suppose that for every positive integer

the integers

and
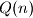
are positive, and
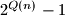
divides
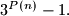
Prove that
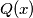
is a constant polynomial.
Proposed by Oleksiy Klurman, Ukraine
%V0
Let $P(x)$ and $Q(x)$ be two polynomials with integer coefficients, such that no nonconstant polynomial with rational coefficients divides both $P(x)$ and $Q(x).$ Suppose that for every positive integer $n$ the integers $P(n)$ and $Q(n)$ are positive, and $2^{Q(n)}-1$ divides $3^{P(n)}-1.$ Prove that $Q(x)$ is a constant polynomial.
Proposed by Oleksiy Klurman, Ukraine