MEMO 2013 ekipno problem 6
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 Neka je točka 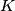 unutar šiljastokutnog trokuta
unutar šiljastokutnog trokuta 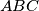 takva da je pravac
takva da je pravac 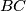 zajednička tangenta kružnica opisanih trokutima
zajednička tangenta kružnica opisanih trokutima 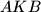 i
i 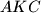 . Neka je točka
. Neka je točka 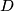 sjecište pravaca
sjecište pravaca 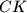 i
i 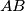 te neka je točka
te neka je točka 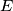 sjecište pravaca
sjecište pravaca 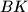 i
i 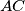 . Neka je točka
. Neka je točka 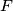 sjecište pravca
sjecište pravca 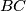 i simetrale dužine
i simetrale dužine 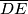 . Opisana kružnica trokuta
. Opisana kružnica trokuta 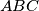 i kružnica
i kružnica 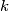 polumjera
polumjera 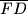 sa središtem u točki
sa središtem u točki 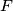 sijeku se u točkama
sijeku se u točkama  i
i 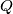 .
.
Dokažite da je dužina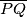 promjer kružnice
promjer kružnice 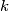 .
.
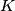 unutar šiljastokutnog trokuta
unutar šiljastokutnog trokuta 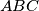 takva da je pravac
takva da je pravac 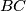 zajednička tangenta kružnica opisanih trokutima
zajednička tangenta kružnica opisanih trokutima 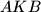 i
i 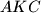 . Neka je točka
. Neka je točka 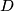 sjecište pravaca
sjecište pravaca 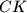 i
i 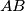 te neka je točka
te neka je točka 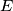 sjecište pravaca
sjecište pravaca 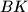 i
i 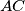 . Neka je točka
. Neka je točka 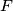 sjecište pravca
sjecište pravca 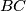 i simetrale dužine
i simetrale dužine 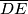 . Opisana kružnica trokuta
. Opisana kružnica trokuta 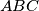 i kružnica
i kružnica 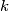 polumjera
polumjera 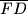 sa središtem u točki
sa središtem u točki 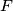 sijeku se u točkama
sijeku se u točkama  i
i 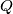 .
.Dokažite da je dužina
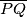 promjer kružnice
promjer kružnice 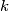 .
. Izvor: Srednjoeuropska matematička olimpijada 2013, ekipno natjecanje, problem 6
 Školjka
Školjka