Školjka

Dan je prirodni broj 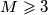$M\geqslant 3$. Kažemo da je pravilni mnogokut \emph{sjajno} obojan ako su sve njegove stranice i dijagonale obojane u točno 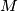$M$ boja tako da ne postoje tri vrha tog mnogokuta koja određuju trokut čije su stranice obojane u točno dvije boje. Neka je 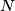$N$ najveći prirodni broj takav da postoji sjajno obojani pravilni mnogokut s točno 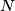$N$ vrhova. a) Dokaži da je 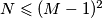$N\leqslant (M-1)^2$.\\ b) Ako je 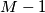$M-1$ prosti broj, dokaži da postoji sjajno obojani pravilni mnogokut s točno 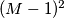$(M-1)^2$ vrhova.