Školjka A set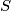 
of points from the space will be called completely symmetric if it has at least three elements and fulfills the condition that for every two distinct points 
and 
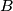from 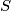, the perpendicular bisector plane of the segment 
is a plane of symmetry for 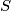. Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, or a regular tetrahedron or a regular octahedron.
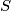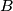of points from the space will be called completely symmetric if it has at least three elements and fulfills the condition that for every two distinct points and from 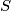, the perpendicular bisector plane of the segment is a plane of symmetry for 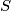. Prove that if a completely symmetric set is finite, then it consists of the vertices of either a regular polygon, or a regular tetrahedron or a regular octahedron.