IMO Shortlist 2004 problem G4
Dodao/la:
arhiva2. travnja 2012. In a convex quadrilateral
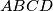
, the diagonal
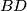
bisects neither the angle
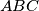
nor the angle
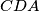
. The point

lies inside
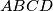
and satisfies
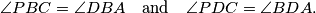
Prove that
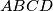
is a cyclic quadrilateral if and only if
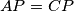
.
%V0
In a convex quadrilateral $ABCD$, the diagonal $BD$ bisects neither the angle $ABC$ nor the angle $CDA$. The point $P$ lies inside $ABCD$ and satisfies $$\angle PBC=\angle DBA \quad \text{and} \quad \angle PDC = \angle BDA.$$
Prove that $ABCD$ is a cyclic quadrilateral if and only if $AP=CP$.
Izvor: Međunarodna matematička olimpijada, shortlist 2004