Školjka

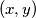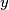\emph{Pozicija} je bilo koja točka $(x, y)$ u ravnini takva da su $x$ i $y$ prirodni brojevi manji ili jednaki od 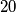$20$.\\ Na početku, svaka od 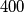$400$ pozicija je slobodna. Ana i Borna igraju igru u kojoj naizmjenično povlače poteze, pri čemu Ana igra prva. U svakom svom potezu Ana postavlja novi crveni kamenčić na slobodnu poziciju tako da je udaljenost bilo koje dvije pozicije na kojima se nalaze crveni kamenčići različita od 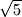$\sqrt{5}$. U svakom svom potezu Borna postavlja novi plavi kamenčić na neku slobodnu poziciju. (Pozicija na kojoj se nalazi plavi kamenčić može biti na bilo kojoj udaljenosti od drugih pozicija na kojima se nalazi neki kamenčić.) Igra se završava kad neki igrač više ne može povući potez.\\\\ Odredi najveći broj 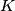$K$ takav da Ana sigurno može postaviti barem 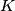$K$ crvenih kamenčića, bez obzira na to kako Borna postavlja svoje plave kamenčiće.