IMO Shortlist 1967 problem 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 (i) Solve the equation:
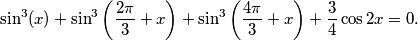
(ii) Supposing the solutions are in the form of arcs with one end at the point
with one end at the point  , the beginning of the arcs of the trigonometric circle, and
, the beginning of the arcs of the trigonometric circle, and  a regular polygon inscribed in the circle with one vertex in
a regular polygon inscribed in the circle with one vertex in  , find:
, find:
1) The subsets of arcs having the other end in in one of the vertices of the regular dodecagon.
in one of the vertices of the regular dodecagon.
2) Prove that no solution can have the end in one of the vertices of polygon
in one of the vertices of polygon  whose number of sides is prime or having factors other than 2 or 3.
whose number of sides is prime or having factors other than 2 or 3.
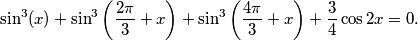
(ii) Supposing the solutions are in the form of arcs
 with one end at the point
with one end at the point  , the beginning of the arcs of the trigonometric circle, and
, the beginning of the arcs of the trigonometric circle, and  a regular polygon inscribed in the circle with one vertex in
a regular polygon inscribed in the circle with one vertex in  , find:
, find: 1) The subsets of arcs having the other end in
 in one of the vertices of the regular dodecagon.
in one of the vertices of the regular dodecagon. 2) Prove that no solution can have the end
 in one of the vertices of polygon
in one of the vertices of polygon  whose number of sides is prime or having factors other than 2 or 3.
whose number of sides is prime or having factors other than 2 or 3. Izvor: Međunarodna matematička olimpijada, shortlist 1967
 Školjka
Školjka 
