IMO Shortlist 1974 problem 5
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let 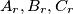 be points on the circumference of a given circle
be points on the circumference of a given circle  . From the triangle
. From the triangle 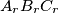 , called
, called 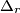 , the triangle
, the triangle 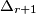 is obtained by constructing the points
is obtained by constructing the points 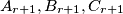 on
on  such that
such that 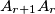 is parallel to
is parallel to 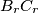 ,
, 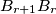 is parallel to
is parallel to 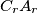 , and
, and 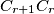 is parallel to
is parallel to 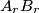 . Each angle of
. Each angle of 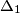 is an integer number of degrees and those integers are not multiples of
is an integer number of degrees and those integers are not multiples of 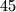 . Prove that at least two of the triangles
. Prove that at least two of the triangles 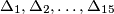 are congruent.
are congruent.
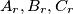 be points on the circumference of a given circle
be points on the circumference of a given circle  . From the triangle
. From the triangle 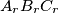 , called
, called 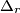 , the triangle
, the triangle 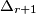 is obtained by constructing the points
is obtained by constructing the points 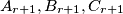 on
on  such that
such that 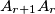 is parallel to
is parallel to 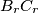 ,
, 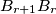 is parallel to
is parallel to 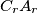 , and
, and 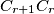 is parallel to
is parallel to 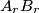 . Each angle of
. Each angle of 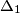 is an integer number of degrees and those integers are not multiples of
is an integer number of degrees and those integers are not multiples of 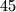 . Prove that at least two of the triangles
. Prove that at least two of the triangles 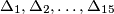 are congruent.
are congruent. Izvor: Međunarodna matematička olimpijada, shortlist 1974
 Školjka
Školjka 
