IMO Shortlist 1995 problem G8
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 Suppose that 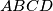 is a cyclic quadrilateral. Let
is a cyclic quadrilateral. Let 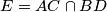 and
and 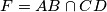 . Denote by
. Denote by 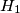 and
and 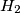 the orthocenters of triangles
the orthocenters of triangles 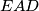 and
and 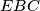 , respectively. Prove that the points
, respectively. Prove that the points 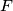 ,
, 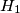 ,
, 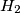 are collinear.
are collinear.
Original formulation:
Let be a triangle. A circle passing through
be a triangle. A circle passing through  and
and 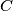 intersects the sides
intersects the sides  and
and 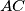 again at
again at 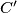 and
and 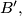 respectively. Prove that
respectively. Prove that 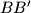 ,
, 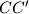 and
and 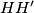 are concurrent, where
are concurrent, where 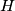 and
and 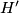 are the orthocentres of triangles
are the orthocentres of triangles  and
and 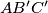 respectively.
respectively.
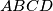 is a cyclic quadrilateral. Let
is a cyclic quadrilateral. Let 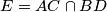 and
and 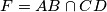 . Denote by
. Denote by 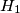 and
and 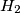 the orthocenters of triangles
the orthocenters of triangles 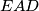 and
and 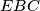 , respectively. Prove that the points
, respectively. Prove that the points 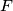 ,
, 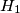 ,
, 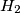 are collinear.
are collinear.Original formulation:
Let
 be a triangle. A circle passing through
be a triangle. A circle passing through  and
and 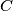 intersects the sides
intersects the sides  and
and 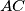 again at
again at 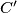 and
and 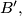 respectively. Prove that
respectively. Prove that 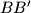 ,
, 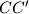 and
and 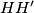 are concurrent, where
are concurrent, where 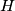 and
and 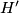 are the orthocentres of triangles
are the orthocentres of triangles  and
and 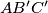 respectively.
respectively. Izvor: Međunarodna matematička olimpijada, shortlist 1995
 Školjka
Školjka 
