IMO Shortlist 2004 problem C1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 There are 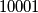 students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of
students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of  societies. Suppose that the following conditions hold:
societies. Suppose that the following conditions hold:
i.) Each pair of students are in exactly one club.
ii.) For each student and each society, the student is in exactly one club of the society.
iii.) Each club has an odd number of students. In addition, a club with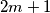 students (
students ( is a positive integer) is
is a positive integer) is
in exactly societies.
societies.
Find all possible values of .
.
RemarkIn IMOTC 2005, it is given that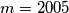 .
.
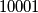 students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of
students at an university. Some students join together to form several clubs (a student may belong to different clubs). Some clubs join together to form several societies (a club may belong to different societies). There are a total of  societies. Suppose that the following conditions hold:
societies. Suppose that the following conditions hold: i.) Each pair of students are in exactly one club.
ii.) For each student and each society, the student is in exactly one club of the society.
iii.) Each club has an odd number of students. In addition, a club with
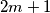 students (
students ( is a positive integer) is
is a positive integer) is in exactly
 societies.
societies. Find all possible values of
 .
. RemarkIn IMOTC 2005, it is given that
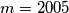 .
. Izvor: Međunarodna matematička olimpijada, shortlist 2004
 Školjka
Školjka 
