IMO Shortlist 2008 problem G2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 Given trapezoid 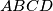 with parallel sides
with parallel sides  and
and 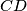 , assume that there exist points
, assume that there exist points 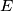 on line
on line  outside segment
outside segment  , and
, and 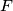 inside segment
inside segment 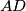 such that
such that 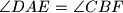 . Denote by
. Denote by  the point of intersection of
the point of intersection of 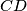 and
and 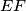 , and by
, and by 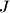 the point of intersection of
the point of intersection of  and
and 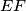 . Let
. Let 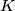 be the midpoint of segment
be the midpoint of segment 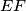 , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 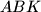 if and only if
if and only if 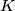 belongs to the circumcircle of
belongs to the circumcircle of 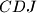 .
.
Proposed by Charles Leytem, Luxembourg
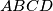 with parallel sides
with parallel sides  and
and 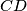 , assume that there exist points
, assume that there exist points 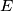 on line
on line  outside segment
outside segment  , and
, and 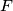 inside segment
inside segment 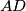 such that
such that 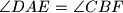 . Denote by
. Denote by  the point of intersection of
the point of intersection of 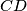 and
and 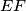 , and by
, and by 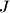 the point of intersection of
the point of intersection of  and
and 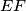 . Let
. Let 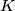 be the midpoint of segment
be the midpoint of segment 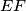 , assume it does not lie on line
, assume it does not lie on line  . Prove that
. Prove that  belongs to the circumcircle of
belongs to the circumcircle of 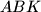 if and only if
if and only if 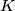 belongs to the circumcircle of
belongs to the circumcircle of 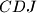 .
. Proposed by Charles Leytem, Luxembourg
Izvor: Međunarodna matematička olimpijada, shortlist 2008
Komentari:
fini_keksi, 22. veljače 2023. 12:13
 Školjka
Školjka 
