IMO Shortlist 2011 problem C5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Let  be a positive integer, and consider a
be a positive integer, and consider a 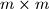 checkerboard consisting of unit squares. At the centre of some of these unit squares there is an ant. At time
checkerboard consisting of unit squares. At the centre of some of these unit squares there is an ant. At time 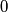 , each ant starts moving with speed
, each ant starts moving with speed 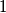 parallel to some edge of the checkerboard. When two ants moving in the opposite directions meet, they both turn
parallel to some edge of the checkerboard. When two ants moving in the opposite directions meet, they both turn 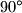 clockwise and continue moving with speed
clockwise and continue moving with speed 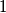 . When more than
. When more than 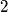 ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear.
ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear.
Considering all possible starting positions, determine the latest possible moment at which the last ant falls off the checkerboard, or prove that such a moment does not necessarily exist.
Proposed by Toomas Krips, Estonia
 be a positive integer, and consider a
be a positive integer, and consider a 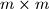 checkerboard consisting of unit squares. At the centre of some of these unit squares there is an ant. At time
checkerboard consisting of unit squares. At the centre of some of these unit squares there is an ant. At time 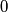 , each ant starts moving with speed
, each ant starts moving with speed 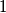 parallel to some edge of the checkerboard. When two ants moving in the opposite directions meet, they both turn
parallel to some edge of the checkerboard. When two ants moving in the opposite directions meet, they both turn 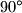 clockwise and continue moving with speed
clockwise and continue moving with speed 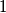 . When more than
. When more than 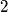 ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear.
ants meet, or when two ants moving in perpendicular directions meet, the ants continue moving in the same direction as before they met. When an ant reaches one of the edges of the checkerboard, it falls off and will not re-appear.Considering all possible starting positions, determine the latest possible moment at which the last ant falls off the checkerboard, or prove that such a moment does not necessarily exist.
Proposed by Toomas Krips, Estonia
Izvor: Međunarodna matematička olimpijada, shortlist 2011
 Školjka
Školjka 
