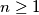
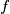
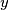
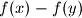
Let be an odd integer. Determine all functions from the set of integers to itself, such that for all integers and the difference divides
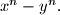
Proposed by Mihai Baluna, Romania
%V0
Let $n \geq 1$ be an odd integer. Determine all functions $f$ from the set of integers to itself, such that for all integers $x$ and $y$ the difference $f(x)-f(y)$ divides $x^n-y^n.$
Proposed by Mihai Baluna, Romania
Izvor: Međunarodna matematička olimpijada, shortlist 2011
Školjka 
be an odd integer. Determine all functions 
from the set of integers to itself, such that for all integers 
and 
the difference 
divides 