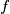
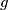
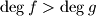
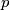
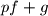
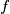
Let and be two nonzero polynomials with integer coefficients and . Suppose that for infinitely many primes the polynomial has a rational root. Prove that has a rational root.
%V0
Let $f$ and $g$ be two nonzero polynomials with integer coefficients and $\deg f>\deg g$. Suppose that for infinitely many primes $p$ the polynomial $pf+g$ has a rational root. Prove that $f$ has a rational root.
Izvor: Međunarodna matematička olimpijada, shortlist 2012
Školjka 
and 
be two nonzero polynomials with integer coefficients and 
. Suppose that for infinitely many primes 
the polynomial 
has a rational root. Prove that