IMO Shortlist 2012 problem C1
Dodao/la:
arhiva3. studenoga 2013. Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers

and
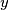
such that
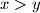
and

is to the left of
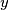
, and replaces the pair
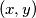
by either
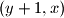
or
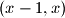
. Prove that she can perform only finitely many such iterations.
Proposed by Warut Suksompong, Thailand
%V0
Several positive integers are written in a row. Iteratively, Alice chooses two adjacent numbers $x$ and $y$ such that $x>y$ and $x$ is to the left of $y$, and replaces the pair $(x,y)$ by either $(y+1,x)$ or $(x-1,x)$. Prove that she can perform only finitely many such iterations.
Proposed by Warut Suksompong, Thailand
Izvor: Međunarodna matematička olimpijada, shortlist 2012