IMO Shortlist 2012 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Players  and
and  play a game with
play a game with 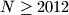 coins and
coins and 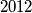 boxes arranged around a circle. Initially
boxes arranged around a circle. Initially  distributes the coins among the boxes so that there is at least
distributes the coins among the boxes so that there is at least 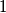 coin in each box. Then the two of them make moves in the order
coin in each box. Then the two of them make moves in the order 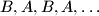 by the following rules:
by the following rules:
(a) On every move of his passes
passes 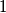 coin from every box to an adjacent box.
coin from every box to an adjacent box.
(b) On every move of hers chooses several coins that were not involved in
chooses several coins that were not involved in  's previous move and are in different boxes. She passes every coin to and adjacent box.
's previous move and are in different boxes. She passes every coin to and adjacent box.
Player 's goal is to ensure at least
's goal is to ensure at least 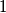 coin in each box after every move of hers, regardless of how
coin in each box after every move of hers, regardless of how  plays and how many moves are made. Find the least
plays and how many moves are made. Find the least  that enables her to succeed.
that enables her to succeed.
 and
and  play a game with
play a game with 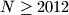 coins and
coins and 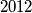 boxes arranged around a circle. Initially
boxes arranged around a circle. Initially  distributes the coins among the boxes so that there is at least
distributes the coins among the boxes so that there is at least 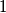 coin in each box. Then the two of them make moves in the order
coin in each box. Then the two of them make moves in the order 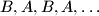 by the following rules:
by the following rules:(a) On every move of his
 passes
passes 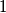 coin from every box to an adjacent box.
coin from every box to an adjacent box.(b) On every move of hers
 chooses several coins that were not involved in
chooses several coins that were not involved in  's previous move and are in different boxes. She passes every coin to and adjacent box.
's previous move and are in different boxes. She passes every coin to and adjacent box.Player
 's goal is to ensure at least
's goal is to ensure at least 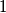 coin in each box after every move of hers, regardless of how
coin in each box after every move of hers, regardless of how  plays and how many moves are made. Find the least
plays and how many moves are made. Find the least  that enables her to succeed.
that enables her to succeed. Izvor: Međunarodna matematička olimpijada, shortlist 2012
 Školjka
Školjka 
