IMO Shortlist 2012 problem G8
Kvaliteta:
Avg: 0,0Težina:
Avg: 9,0 Let  be a triangle with circumcircle
be a triangle with circumcircle 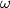 and
and 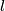 a line without common points with
a line without common points with 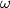 . Denote by
. Denote by  the foot of the perpendicular from the center of
the foot of the perpendicular from the center of 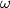 to
to 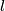 . The side-lines
. The side-lines 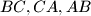 intersect
intersect 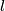 at the points
at the points 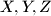 different from
different from  . Prove that the circumcircles of the triangles
. Prove that the circumcircles of the triangles 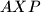 ,
, 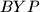 and
and 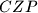 have a common point different from
have a common point different from  or are mutually tangent at
or are mutually tangent at  .
.
 be a triangle with circumcircle
be a triangle with circumcircle 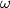 and
and 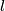 a line without common points with
a line without common points with 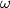 . Denote by
. Denote by  the foot of the perpendicular from the center of
the foot of the perpendicular from the center of 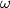 to
to 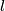 . The side-lines
. The side-lines 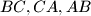 intersect
intersect 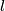 at the points
at the points 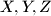 different from
different from  . Prove that the circumcircles of the triangles
. Prove that the circumcircles of the triangles 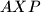 ,
, 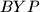 and
and 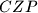 have a common point different from
have a common point different from  or are mutually tangent at
or are mutually tangent at  .
. Izvor: Međunarodna matematička olimpijada, shortlist 2012
 Školjka
Školjka 
