For a sequence 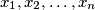 of real numbers, we define its price as
of real numbers, we define its price as 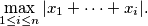
Given  real numbers, Dave and George want to arrange them into a sequence with a low price. Diligent Dave checks all possible ways and finds the minimum possible price
real numbers, Dave and George want to arrange them into a sequence with a low price. Diligent Dave checks all possible ways and finds the minimum possible price 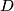 . Greedy George, on the other hand, chooses
. Greedy George, on the other hand, chooses 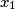 such that
such that 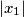 is as small as possible; among the remaining numbers, he chooses
is as small as possible; among the remaining numbers, he chooses 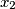 such that
such that 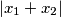 is as small as possible, and so on. Thus, in the
is as small as possible, and so on. Thus, in the 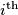 step he chooses
step he chooses 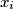 among the remaining numbers so as to minimise the value of
among the remaining numbers so as to minimise the value of 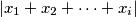 . In each step, if several numbers provide the same value, George chooses one at random. Finally he gets a sequence with price
. In each step, if several numbers provide the same value, George chooses one at random. Finally he gets a sequence with price 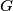 .
.
Find the least possible constant  such that for every positive integer
such that for every positive integer  , for every collection of
, for every collection of  real numbers, and for every possible sequence that George might obtain, the resulting values satisfy the inequality
real numbers, and for every possible sequence that George might obtain, the resulting values satisfy the inequality 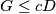 .
.
For a sequence $x_1, x_2, \ldots, x_n$ of real numbers, we define its \emph{price} as
$$ \max_{1 \leq i \leq n} |x_1 + \dots + x_i| \text{.} $$
Given $n$ real numbers, Dave and George want to arrange them into a sequence with a low price. Diligent Dave checks all possible ways and finds the minimum possible price $D$. Greedy George, on the other hand, chooses $x_1$ such that $|x_1|$ is as small as possible; among the remaining numbers, he chooses $x_2$ such that $|x_1 + x_2|$ is as small as possible, and so on. Thus, in the $i^{\text{th}}$ step he chooses $x_i$ among the remaining numbers so as to minimise the value of $|x_1 + x_2 + \dots + x_i|$. In each step, if several numbers provide the same value, George chooses one at random. Finally he gets a sequence with price $G$.
Find the least possible constant $c$ such that for every positive integer $n$, for every collection of $n$ real numbers, and for every possible sequence that George might obtain, the resulting values satisfy the inequality $G \leq c D$.
\begin{flushright}\emph{(Georgia)}\end{flushright}
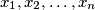 of real numbers, we define its price as
of real numbers, we define its price as 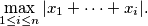
 real numbers, Dave and George want to arrange them into a sequence with a low price. Diligent Dave checks all possible ways and finds the minimum possible price
real numbers, Dave and George want to arrange them into a sequence with a low price. Diligent Dave checks all possible ways and finds the minimum possible price 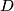 . Greedy George, on the other hand, chooses
. Greedy George, on the other hand, chooses 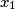 such that
such that 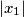 is as small as possible; among the remaining numbers, he chooses
is as small as possible; among the remaining numbers, he chooses 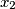 such that
such that 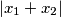 is as small as possible, and so on. Thus, in the
is as small as possible, and so on. Thus, in the 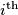 step he chooses
step he chooses 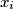 among the remaining numbers so as to minimise the value of
among the remaining numbers so as to minimise the value of 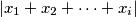 . In each step, if several numbers provide the same value, George chooses one at random. Finally he gets a sequence with price
. In each step, if several numbers provide the same value, George chooses one at random. Finally he gets a sequence with price 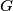 .
. such that for every positive integer
such that for every positive integer  , for every collection of
, for every collection of  real numbers, and for every possible sequence that George might obtain, the resulting values satisfy the inequality
real numbers, and for every possible sequence that George might obtain, the resulting values satisfy the inequality 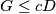 .
. Školjka
Školjka 
