Školjka

Consider 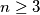$n \geq 3$ lines in the plane such that no two lines are parallel and no three have a common point. These lines divide the plane into polygonal regions; let 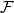$\mathcal{F}$ be the set of regions having finite area. Prove that it is possible to colour 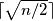$\lceil \sqrt{n / 2} \rceil$ of the lines blue in such a way that no region in 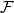$\mathcal{F}$ has a completely blue boundary. (For a real number 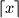$x$, $\lceil x \rceil$ denotes the least integer which is not smaller than $x$.) \begin{flushright}\emph{(Austria)}\end{flushright}