IMO Shortlist 2015 problem C3
Kvaliteta:
Avg: 3,0Težina:
Avg: 6,5For a finite set  of positive integers, a partition of
of positive integers, a partition of  into two disjoint nonempty subsets
into two disjoint nonempty subsets 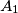 and
and  is
is 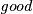 if the least common multiple of the elements in
if the least common multiple of the elements in 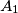 is equal to the greatest common divisor of the elements in
is equal to the greatest common divisor of the elements in  . Determine the minimum value of
. Determine the minimum value of  such that there exists a set of
such that there exists a set of  positive integers with exactly
positive integers with exactly 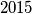 good partitions.
good partitions.
(Ukraine)
Izvor: https://www.imo-official.org/problems/IMO2015SL.pdf
 Školjka
Školjka 
