Školjka

Consider 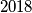$2018$ pairwise crossing circles no three of which are concurrent. These circles subdivide the plane into regions bounded by circular 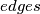$edges$ that meet at 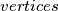$vertices$. Notice that there are an even number of vertices on each circle. Given the circle, alternately colour the vertices on that circle red and blue. In doing so for each circle, every vertex is coloured twice- once for each of the two circle that cross at that point. If the two colours agree at a vertex, then it is assigned that colour; otherwise, it becomes yellow. Show that, if some circle contains at least 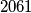$2061$ yellow points, then the vertices of some region are all yellow.