IMO Shortlist 1968 problem 8
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Given an oriented line 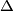 and a fixed point
and a fixed point  on it, consider all trapezoids
on it, consider all trapezoids 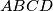 one of whose bases
one of whose bases  lies on
lies on 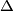 , in the positive direction. Let
, in the positive direction. Let 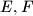 be the midpoints of
be the midpoints of  and
and 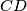 respectively. Find the loci of vertices
respectively. Find the loci of vertices 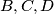 of trapezoids that satisfy the following:
of trapezoids that satisfy the following:
(i)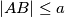 (
( fixed);
fixed);
(ii)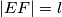 (
(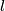 fixed);
fixed);
(iii) the sum of squares of the nonparallel sides of the trapezoid is constant.
Remark
Remark. The constants are chosen so that such trapezoids exist.
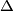 and a fixed point
and a fixed point  on it, consider all trapezoids
on it, consider all trapezoids 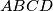 one of whose bases
one of whose bases  lies on
lies on 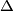 , in the positive direction. Let
, in the positive direction. Let 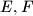 be the midpoints of
be the midpoints of  and
and 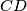 respectively. Find the loci of vertices
respectively. Find the loci of vertices 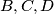 of trapezoids that satisfy the following:
of trapezoids that satisfy the following:(i)
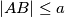 (
( fixed);
fixed);(ii)
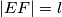 (
(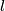 fixed);
fixed);(iii) the sum of squares of the nonparallel sides of the trapezoid is constant.
Remark
Remark. The constants are chosen so that such trapezoids exist.
Izvor: Međunarodna matematička olimpijada, shortlist 1968
 Školjka
Školjka