IMO Shortlist 1969 problem 14
Dodao/la:
arhiva2. travnja 2012. 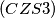
Let

and

be two positive real numbers. If

is a real solution of the equation
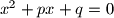
with real coefficients
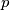
and
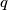
such that
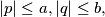
prove that
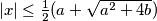
Conversely, if

satisfies the above inequality, prove that there exist real numbers
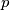
and
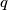
with
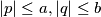
such that

is one of the roots of the equation
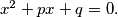
%V0
$(CZS 3)$ Let $a$ and $b$ be two positive real numbers. If $x$ is a real solution of the equation $x^2 + px + q = 0$ with real coefficients $p$ and $q$ such that $|p| \le a, |q| \le b,$ prove that $|x| \le \frac{1}{2}(a +\sqrt{a^2 + 4b})$ Conversely, if $x$ satisfies the above inequality, prove that there exist real numbers $p$ and
$q$ with $|p|\le a, |q|\le b$ such that $x$ is one of the roots of the equation $x^2+px+ q = 0.$
Izvor: Međunarodna matematička olimpijada, shortlist 1969