IMO Shortlist 1973 problem 4
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Let  be a set of
be a set of 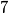 different prime numbers and
different prime numbers and  a set of
a set of 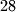 different composite numbers each of which is a product of two (not necessarily different) numbers from
different composite numbers each of which is a product of two (not necessarily different) numbers from  . The set
. The set  is divided into
is divided into 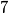 disjoint four-element subsets such that each of the numbers in one set has a common prime divisor with at least two other numbers in that set. How many such partitions of
disjoint four-element subsets such that each of the numbers in one set has a common prime divisor with at least two other numbers in that set. How many such partitions of  are there ?
are there ?
 be a set of
be a set of 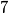 different prime numbers and
different prime numbers and  a set of
a set of 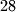 different composite numbers each of which is a product of two (not necessarily different) numbers from
different composite numbers each of which is a product of two (not necessarily different) numbers from  . The set
. The set  is divided into
is divided into 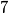 disjoint four-element subsets such that each of the numbers in one set has a common prime divisor with at least two other numbers in that set. How many such partitions of
disjoint four-element subsets such that each of the numbers in one set has a common prime divisor with at least two other numbers in that set. How many such partitions of  are there ?
are there ? Izvor: Međunarodna matematička olimpijada, shortlist 1973
 Školjka
Školjka