IMO Shortlist 1987 problem 2
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 At a party attended by  married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques
married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques 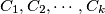 with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if
with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if 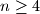 , then
, then 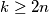 .
.
Proposed by USA.
 married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques
married couples, each person talks to everyone else at the party except his or her spouse. The conversations involve sets of persons or cliques 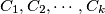 with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if
with the following property: no couple are members of the same clique, but for every other pair of persons there is exactly one clique to which both members belong. Prove that if 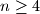 , then
, then 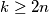 .
.Proposed by USA.
Izvor: Međunarodna matematička olimpijada, shortlist 1987
 Školjka
Školjka 
