IMO Shortlist 1991 problem 1
Kvaliteta:
Avg: 0,0Težina:
Avg: 0,0 Given a point  inside a triangle
inside a triangle 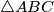 . Let
. Let 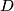 ,
, 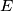 ,
, 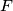 be the orthogonal projections of the point
be the orthogonal projections of the point  on the sides
on the sides  ,
, 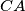 ,
,  , respectively. Let the orthogonal projections of the point
, respectively. Let the orthogonal projections of the point  on the lines
on the lines 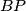 and
and 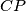 be
be  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 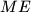 ,
, 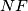 ,
,  are concurrent.
are concurrent.
Original formulation:
Let be any triangle and
be any triangle and  any point in its interior. Let
any point in its interior. Let 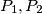 be the feet of the perpendiculars from
be the feet of the perpendiculars from  to the two sides
to the two sides 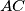 and
and 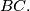 Draw
Draw 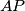 and
and 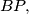 and from
and from 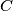 drop perpendiculars to
drop perpendiculars to 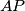 and
and 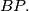 Let
Let 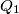 and
and 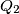 be the feet of these perpendiculars. Prove that the lines
be the feet of these perpendiculars. Prove that the lines 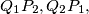 and
and  are concurrent.
are concurrent.
 inside a triangle
inside a triangle 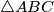 . Let
. Let 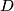 ,
, 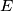 ,
, 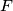 be the orthogonal projections of the point
be the orthogonal projections of the point  on the sides
on the sides  ,
, 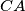 ,
,  , respectively. Let the orthogonal projections of the point
, respectively. Let the orthogonal projections of the point  on the lines
on the lines 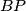 and
and 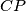 be
be  and
and  , respectively. Prove that the lines
, respectively. Prove that the lines 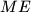 ,
, 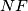 ,
,  are concurrent.
are concurrent. Original formulation:
Let
 be any triangle and
be any triangle and  any point in its interior. Let
any point in its interior. Let 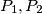 be the feet of the perpendiculars from
be the feet of the perpendiculars from  to the two sides
to the two sides 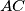 and
and 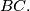 Draw
Draw 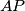 and
and 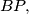 and from
and from 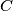 drop perpendiculars to
drop perpendiculars to 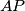 and
and 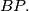 Let
Let 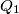 and
and 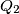 be the feet of these perpendiculars. Prove that the lines
be the feet of these perpendiculars. Prove that the lines 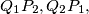 and
and  are concurrent.
are concurrent. Izvor: Međunarodna matematička olimpijada, shortlist 1991
 Školjka
Školjka 
