IMO Shortlist 1993 problem N4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Let 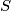 be the set of all pairs
be the set of all pairs 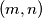 of relatively prime positive integers
of relatively prime positive integers 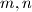 with
with  even and
even and 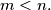 For
For 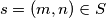 write
write 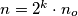 where
where 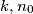 are positive integers with
are positive integers with 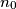 odd and define
odd and define 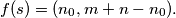 Prove that
Prove that 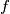 is a function from
is a function from 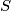 to
to 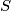 and that for each
and that for each 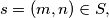 there exists a positive integer
there exists a positive integer 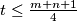 such that
such that 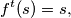 where
where 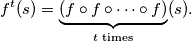
If is a prime number which does not divide
is a prime number which does not divide 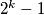 for
for 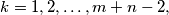 prove that the smallest value
prove that the smallest value 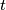 which satisfies the above conditions is
which satisfies the above conditions is ![\left [\frac{m+n+1}{4} \right ]](/media/m/8/7/8/878d7261cbd40fe8c838d36d2b94fea7.png) where
where ![\left[ x \right]](/media/m/8/4/7/847a3b7449538c2b99179a2953e7f9e0.png) denotes the greatest integer
denotes the greatest integer 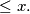
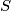 be the set of all pairs
be the set of all pairs 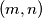 of relatively prime positive integers
of relatively prime positive integers 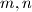 with
with  even and
even and 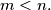 For
For 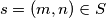 write
write 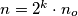 where
where 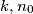 are positive integers with
are positive integers with 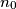 odd and define
odd and define 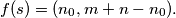 Prove that
Prove that 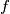 is a function from
is a function from 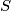 to
to 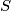 and that for each
and that for each 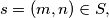 there exists a positive integer
there exists a positive integer 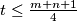 such that
such that 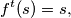 where
where 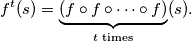
If
 is a prime number which does not divide
is a prime number which does not divide 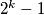 for
for 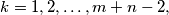 prove that the smallest value
prove that the smallest value 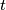 which satisfies the above conditions is
which satisfies the above conditions is ![\left [\frac{m+n+1}{4} \right ]](/media/m/8/7/8/878d7261cbd40fe8c838d36d2b94fea7.png) where
where ![\left[ x \right]](/media/m/8/4/7/847a3b7449538c2b99179a2953e7f9e0.png) denotes the greatest integer
denotes the greatest integer 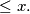
Izvor: Međunarodna matematička olimpijada, shortlist 1993
 Školjka
Školjka