IMO Shortlist 1995 problem G3
Dodao/la:
arhiva2. travnja 2012. The incircle of triangle
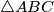
touches the sides

,
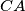
,

at
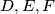
respectively.
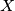
is a point inside triangle of
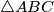
such that the incircle of triangle

touches

at
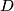
, and touches
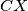
and
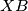
at
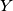
and
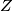
respectively.
Show that
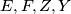
are concyclic.
%V0
The incircle of triangle $\triangle ABC$ touches the sides $BC$, $CA$, $AB$ at $D, E, F$ respectively. $X$ is a point inside triangle of $\triangle ABC$ such that the incircle of triangle $\triangle XBC$ touches $BC$ at $D$, and touches $CX$ and $XB$ at $Y$ and $Z$ respectively.
Show that $E, F, Z, Y$ are concyclic.
Izvor: Međunarodna matematička olimpijada, shortlist 1995