IMO Shortlist 1996 problem C2
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 A square  is divided into
is divided into 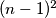 unit squares in the usual manner. Each of the
unit squares in the usual manner. Each of the 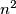 vertices of these squares is to be coloured red or blue. Find the number of different colourings such that each unit square has exactly two red vertices. (Two colouring schemse are regarded as different if at least one vertex is coloured differently in the two schemes.)
vertices of these squares is to be coloured red or blue. Find the number of different colourings such that each unit square has exactly two red vertices. (Two colouring schemse are regarded as different if at least one vertex is coloured differently in the two schemes.)
 is divided into
is divided into 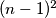 unit squares in the usual manner. Each of the
unit squares in the usual manner. Each of the 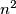 vertices of these squares is to be coloured red or blue. Find the number of different colourings such that each unit square has exactly two red vertices. (Two colouring schemse are regarded as different if at least one vertex is coloured differently in the two schemes.)
vertices of these squares is to be coloured red or blue. Find the number of different colourings such that each unit square has exactly two red vertices. (Two colouring schemse are regarded as different if at least one vertex is coloured differently in the two schemes.) Izvor: Međunarodna matematička olimpijada, shortlist 1996
 Školjka
Školjka 
