IMO Shortlist 1996 problem G1
Kvaliteta:
Avg: 5,0Težina:
Avg: 5,0 Let 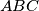 be a triangle, and
be a triangle, and 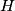 its orthocenter. Let
its orthocenter. Let  be a point on the circumcircle of triangle
be a point on the circumcircle of triangle 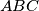 (distinct from the vertices
(distinct from the vertices  ,
, 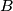 ,
,  ), and let
), and let 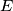 be the foot of the altitude of triangle
be the foot of the altitude of triangle 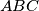 from the vertex
from the vertex 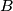 . Let the parallel to the line
. Let the parallel to the line 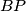 through the point
through the point  meet the parallel to the line
meet the parallel to the line 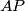 through the point
through the point 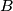 at a point
at a point 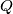 . Let the parallel to the line
. Let the parallel to the line 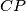 through the point
through the point  meet the parallel to the line
meet the parallel to the line 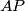 through the point
through the point  at a point
at a point 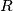 . The lines
. The lines 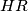 and
and 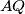 intersect at some point
intersect at some point 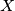 . Prove that the lines
. Prove that the lines 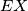 and
and 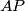 are parallel.
are parallel.
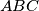 be a triangle, and
be a triangle, and 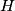 its orthocenter. Let
its orthocenter. Let  be a point on the circumcircle of triangle
be a point on the circumcircle of triangle 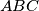 (distinct from the vertices
(distinct from the vertices  ,
,  ,
,  ), and let
), and let 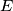 be the foot of the altitude of triangle
be the foot of the altitude of triangle 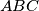 from the vertex
from the vertex 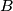 . Let the parallel to the line
. Let the parallel to the line 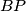 through the point
through the point  meet the parallel to the line
meet the parallel to the line 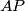 through the point
through the point 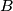 at a point
at a point 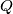 . Let the parallel to the line
. Let the parallel to the line 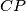 through the point
through the point  meet the parallel to the line
meet the parallel to the line 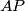 through the point
through the point  at a point
at a point 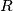 . The lines
. The lines 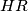 and
and 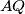 intersect at some point
intersect at some point 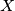 . Prove that the lines
. Prove that the lines 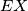 and
and 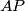 are parallel.
are parallel. Izvor: Međunarodna matematička olimpijada, shortlist 1996
 Školjka
Školjka