IMO Shortlist 1998 problem C1
Kvaliteta:
Avg: 0,0Težina:
Avg: 6,0 A rectangular array of numbers is given. In each row and each column, the sum of all numbers is an integer. Prove that each nonintegral number  in the array can be changed into either
in the array can be changed into either  or
or 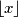 so that the row-sums and column-sums remain unchanged. (Note that
so that the row-sums and column-sums remain unchanged. (Note that  is the least integer greater than or equal to
is the least integer greater than or equal to  , while
, while 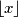 is the greatest integer less than or equal to
is the greatest integer less than or equal to  .)
.)
 in the array can be changed into either
in the array can be changed into either  or
or 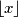 so that the row-sums and column-sums remain unchanged. (Note that
so that the row-sums and column-sums remain unchanged. (Note that  is the least integer greater than or equal to
is the least integer greater than or equal to  , while
, while 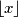 is the greatest integer less than or equal to
is the greatest integer less than or equal to  .)
.) Izvor: Međunarodna matematička olimpijada, shortlist 1998
 Školjka
Školjka 
