IMO Shortlist 1998 problem C4
Kvaliteta:
Avg: 0,0Težina:
Avg: 7,0 Let 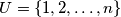 , where
, where 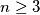 . A subset
. A subset  of
of 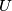 is said to be split by an arrangement of the elements of
is said to be split by an arrangement of the elements of 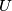 if an element not in
if an element not in  occurs in the arrangement somewhere between two elements of
occurs in the arrangement somewhere between two elements of  . For example, 13542 splits
. For example, 13542 splits 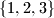 but not
but not 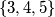 . Prove that for any
. Prove that for any  subsets of
subsets of 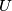 , each containing at least 2 and at most
, each containing at least 2 and at most 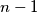 elements, there is an arrangement of the elements of
elements, there is an arrangement of the elements of 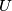 which splits all of them.
which splits all of them.
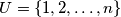 , where
, where 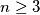 . A subset
. A subset  of
of 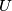 is said to be split by an arrangement of the elements of
is said to be split by an arrangement of the elements of 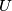 if an element not in
if an element not in  occurs in the arrangement somewhere between two elements of
occurs in the arrangement somewhere between two elements of  . For example, 13542 splits
. For example, 13542 splits 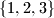 but not
but not 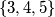 . Prove that for any
. Prove that for any  subsets of
subsets of 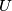 , each containing at least 2 and at most
, each containing at least 2 and at most 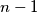 elements, there is an arrangement of the elements of
elements, there is an arrangement of the elements of 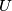 which splits all of them.
which splits all of them. Izvor: Međunarodna matematička olimpijada, shortlist 1998
 Školjka
Školjka 
