IMO Shortlist 2005 problem N5
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Denote by 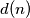 the number of divisors of the positive integer
the number of divisors of the positive integer  . A positive integer
. A positive integer  is called highly divisible if
is called highly divisible if 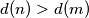 for all positive integers
for all positive integers 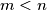 .
.
Two highly divisible integers and
and  with
with 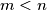 are called consecutive if there exists no highly divisible integer
are called consecutive if there exists no highly divisible integer  satisfying
satisfying 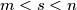 .
.
(a) Show that there are only finitely many pairs of consecutive highly divisible
integers of the form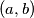 with
with 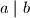 .
.
(b) Show that for every prime number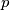 there exist infinitely many positive highly divisible integers
there exist infinitely many positive highly divisible integers  such that
such that 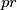 is also highly divisible.
is also highly divisible.
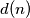 the number of divisors of the positive integer
the number of divisors of the positive integer  . A positive integer
. A positive integer  is called highly divisible if
is called highly divisible if 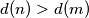 for all positive integers
for all positive integers 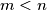 .
. Two highly divisible integers
 and
and  with
with 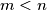 are called consecutive if there exists no highly divisible integer
are called consecutive if there exists no highly divisible integer  satisfying
satisfying 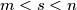 .
. (a) Show that there are only finitely many pairs of consecutive highly divisible
integers of the form
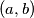 with
with 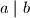 .
. (b) Show that for every prime number
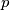 there exist infinitely many positive highly divisible integers
there exist infinitely many positive highly divisible integers  such that
such that 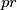 is also highly divisible.
is also highly divisible. Izvor: Međunarodna matematička olimpijada, shortlist 2005
 Školjka
Školjka