IMO Shortlist 2006 problem C1
Kvaliteta:
Avg: 4,0Težina:
Avg: 6,0 We have 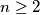 lamps
lamps 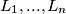 in a row, each of them being either on or off. Every second we simultaneously modify the state of each lamp as follows: if the lamp
in a row, each of them being either on or off. Every second we simultaneously modify the state of each lamp as follows: if the lamp 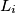 and its neighbours (only one neighbour for
and its neighbours (only one neighbour for 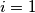 or
or 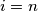 , two neighbours for other
, two neighbours for other 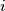 ) are in the same state, then
) are in the same state, then 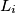 is switched off; – otherwise,
is switched off; – otherwise, 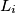 is switched on.
is switched on.
Initially all the lamps are off except the leftmost one which is on.
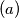 Prove that there are infinitely many integers
Prove that there are infinitely many integers  for which all the lamps will eventually be off.
for which all the lamps will eventually be off.
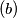 Prove that there are infinitely many integers
Prove that there are infinitely many integers  for which the lamps will never be all off.
for which the lamps will never be all off.
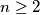 lamps
lamps 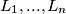 in a row, each of them being either on or off. Every second we simultaneously modify the state of each lamp as follows: if the lamp
in a row, each of them being either on or off. Every second we simultaneously modify the state of each lamp as follows: if the lamp 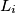 and its neighbours (only one neighbour for
and its neighbours (only one neighbour for 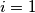 or
or 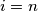 , two neighbours for other
, two neighbours for other 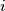 ) are in the same state, then
) are in the same state, then 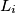 is switched off; – otherwise,
is switched off; – otherwise, 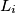 is switched on.
is switched on. Initially all the lamps are off except the leftmost one which is on.
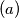 Prove that there are infinitely many integers
Prove that there are infinitely many integers  for which all the lamps will eventually be off.
for which all the lamps will eventually be off. 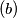 Prove that there are infinitely many integers
Prove that there are infinitely many integers  for which the lamps will never be all off.
for which the lamps will never be all off. Izvor: Međunarodna matematička olimpijada, shortlist 2006
 Školjka
Školjka 
