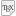IMO Shortlist 2006 problem C6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 A holey triangle is an upward equilateral triangle of side length  with
with  upward unit triangular holes cut out. A diamond is a
upward unit triangular holes cut out. A diamond is a 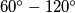 unit rhombus.
unit rhombus.
Prove that a holey triangle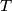 can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length
can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length 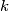 in
in 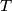 contains at most
contains at most 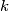 holes, for
holes, for 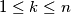 .
.
 with
with  upward unit triangular holes cut out. A diamond is a
upward unit triangular holes cut out. A diamond is a 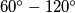 unit rhombus.
unit rhombus. Prove that a holey triangle
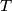 can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length
can be tiled with diamonds if and only if the following condition holds: Every upward equilateral triangle of side length 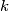 in
in 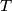 contains at most
contains at most 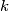 holes, for
holes, for 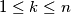 .
. Izvor: Međunarodna matematička olimpijada, shortlist 2006
 Školjka
Školjka